Table of Contents
Estimating the number of unique passwords in the world
Extract the available unique/total counts and ratios
Let's use RockYou:
$ wc -l r 32603387 r $ sort -uS 4G r | wc -l 14344391 $ shuf r > rs # Sanity check $ wc -l rs 32603388 rs # Apparently, "wc -l" didn't count the last line before "shuf" because there was no linefeed character after it. A very minor discrepancy, OK to ignore. $ sort -uS 4G rs | wc -l 14344391 $ head -32603 rs | sort -uS 4G | wc -l 28815 $ head -326034 rs | sort -uS 4G | wc -l 247675 $ head -3260339 rs | sort -uS 4G | wc -l 1976676 # Calculate the ratios $ bc scale=10 28815/32603 .8838143729 247675/326034 .7596600354 1976676/3260339 .6062792856 14344391/32603387 .4399662832
Extrapolate to higher totals
Let's go to Wolfram Alpha and extrapolate:
FindFit[{{32603,28815},{326034,247675},{3260339,1976676},{32603387,14344391}},a x^b,{a,b},x]
FindFit[{{32603,28815},{326034,247675},{3260339,1976676},{32603387,14344391}},a x^b log x,{a,b},x]
FindFit[{{32603,0.883814},{326034,0.75966},{3260339,0.606279},{32603387,0.439966}},{(1+log(1+x/a))^b,b<0,(1+log(1+32603387/a))^b=0.439966},{a,b},x]
FindFit[{{32603,0.883814},{326034,0.75966},{3260339,0.606279},{32603387,0.439966}},{(1+log(1+x/a)/10)^b,b<0,(1+log(1+3260339/a)/10)^b=0.606279,(1+log(1+32603387/a)/10)^b=0.439966},{a,b},x]
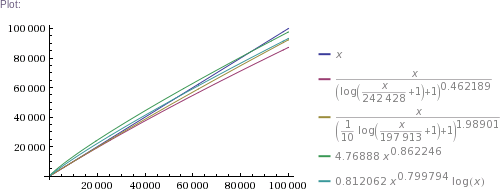
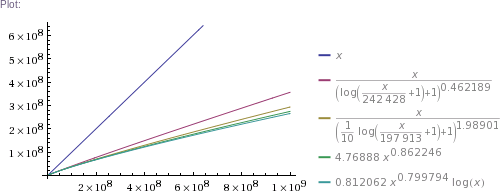
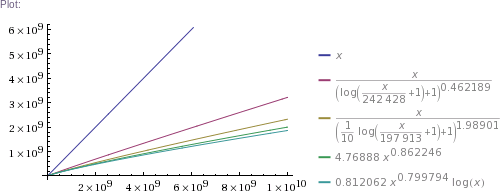
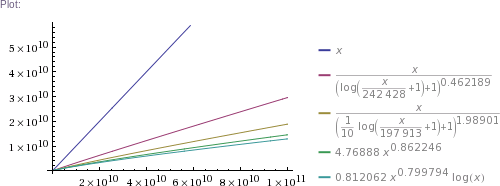
Table[{x((1+log(1+x/242428))^-0.462189),x((1+log(1+x/197913)/10)^-1.98901),4.76888 x^0.862246,0.812062 x^0.799794 log x},{x,{1,1000,32603,10^5,326034,3260339,32603387,10^9,10^10,10^11}}]
Plot[{x,x((1+log(1+x/242428))^-0.462189),x((1+log(1+x/197913)/10)^-1.98901),4.76888 x^0.862246,0.812062 x^0.799794 log x},{x,1,10^5}]
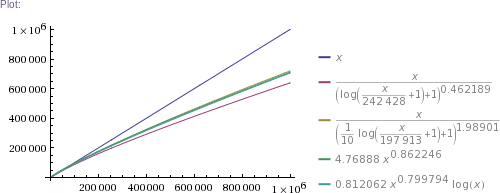
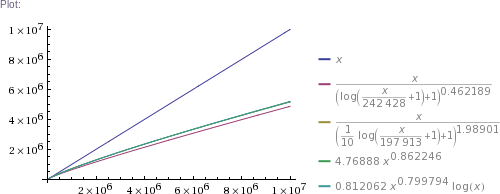
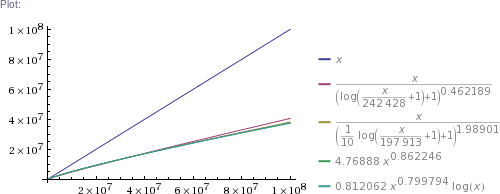
# ... and so on for other plot scales, up to x=10^11
Update: the longest FindFit above may be simplified to:
FindFit[{{3260339,0.606279},{32603387,0.439966}},{(1+log(1+x/a)/10)^b,b<0},{a,b},x]
which gives almost the same result (a=197787 b=-1.9888). With either, we're essentially solving two equations with two unknowns.
Further, when fitting the curve to only 3 points, Wolfram Alpha is able to find three parameters at once, which lets us do:
FindFit[{{326034,0.75966},{3260339,0.606279},{32603387,0.439966}},{(1+a log(1+x/b))^c,c<0},{a,b,c},x]
FindFit[{{326034,0.75966},{3260339,0.606279},{32603387,0.439966}},{(1+log(1+x/b)/a)^c,c<0},{a,b,c},x]
Table[{x((1+0.00799391 log(1+x/35208.8))^-14.8322),x((1+log(1+x/1891.9)/209.283)^-15.0619)},{x,{1,1000,32603,10^5,326034,3260339,32603387,10^9,10^10,10^11}}]
This looks like it'd match our data really well (including in the 1 to 326k range not explicitly included in the FindFit queries), but unfortunately at these parameter values (a power of -15) things get somewhat less stable (precision loss?) We might need to use a better tool for this. The table and graphs below do not use these 3-parameter formulas.
In plain English: we got four pretty good approximation formulas, which produce values matching RockYou's nearly perfectly in the ~300k to 32.6M range. (The simpler two formulas produce impossible values in the 1 to 100k range, though. The more complicated two are chosen such that they can't produce theoretically impossible values, but they nevertheless do produce higher than RockYou's actual numbers of unique passwords in the ~100 to ~200k range.) Then we use these formulas to extrapolate to up to 100 billion of total passwords.
Results
Some numbers of interest: at 1 billion total, there are estimated to be about 300 million unique passwords. At 10 billion, there are ~2.3 billion uniques. At 100 billion, there are ~18 billion uniques. (This is using mean values of the four formulas' results.)
Limitations
A flaw of this approach: the world is not a service like RockYou. Presumably, most people who let RockYou have a password of theirs did so for only one or a few of their passwords, for specific services. Those same people generally also have other password-protected resources, and on at least some of those they might reuse the same passwords. Thus, if we analyzed the full set of {resource, password} combinations of those same people, we'd likely see more duplicate passwords, and would extrapolate to fewer unique passwords in the world. Another way to look at this, though, is that we might be estimating the number of unique passwords in use by a certain number of people (our “total”) rather than among a certain number of {resource, password} combinations.
Adobe leak
The above analysis was based on the RockYou leak. In the ECB mode encrypted passwords leak from Adobe that occurred later, there are about 130 million passwords total, 56 million unique (the exact passwords aren't always known to us, but ECB mode lets us figure out how many are unique anyway). Extrapolation from RockYou using the formulas above gives 47 million to 52 million unique, so Adobe's 56 million suggests that their users' passwords are slightly better in this respect.
Pwned Passwords (HIBP)
Pwned Passwords is a curated and regularly updated collection of leaked/breached plain text passwords redistributed in form of SHA-1 and NTLM hashes for the purpose of detecting and preventing password reuse. It was introduced in August 2017 (many years later than the above analysis of RockYou). Version 7 released in November 2020 contains over 613 million (613584246) hashes of unique passwords. Helpfully, included with each hash is “a count of how many times that password had been seen in the source data breaches.” Adding those up yields over 3.65 billion (3650716681).
Extrapolation from RockYou using the formulas above gives 795 to 1225 million unique, with mean for the four formulas at 935 million. This is the opposite from what we saw in the Adobe leak - Pwned Passwords appear to be significantly worse than RockYou (fewer unique).
To confirm that it's indeed Pwned Passwords being more repetitive than RockYou rather than the extrapolation failing at these numbers of passwords, let's take the first 14344391 lines (same as RockYou unique password count) from pwned-passwords-ntlm-ordered-by-hash-v7.txt and add up the counts on those. Turns out they correspond to 81548722 original passwords (including duplicates), which is 2.5x higher than RockYou's. (Going with the last 14344391 lines instead gives 84209109, which is similar enough. Ideally, we'd shuffle the file first, but since there's no reason to expect password complexity or number of occurrences in a plain text leak to correlate with NTLM hash value, these shortcut approaches work just as well. Sorting by hash value effectively is random shuffling of the password counts.)
Going the other way, it takes about 5.6M lines from pwned-passwords-ntlm-ordered-by-hash-v7.txt, which is about 2.5x lower than RockYou's unique password count of 14.3M, to achieve RockYou's original password count of 32.6M (including duplicates).
Perl script
Perl script to calculate unique from total using the four formulas, as well as average and mean:
#!/usr/bin/perl die "Usage: $0 TOTAL\n" unless ($#ARGV eq 0); $x = $ARGV[0]; $a = $x * ((1 + log(1 + $x / 242428)) ** -0.462189); $b = $x * ((1 + log(1 + $x / 197913) / 10) ** -1.98901); $c = 4.76888 * $x ** 0.862246; $d = 0.812062 * $x ** 0.799794 * log($x); $avg = ($a + $b + $c + $d) / 4; $mean = ($a * $b * $c * $d) ** (1 / 4); printf "%.0f %.0f %.0f %.0f\naverage = %.0f\nmean = %.0f\n", $a, $b, $c, $d, $avg, $mean;
Back to my pseudo homepage.